利用手机与电脑在宿舍内测量声速

Wallbreaker5th大约 5 分钟

注

该实验在 4 月 10 日晚九点左右在合肥进行。现场并没有测量室温的设备。文中某些数据处理可能不严谨。

注

TODO: 使用 Markdown 扩展来重置文中图表。

提示

文中图表不适合在夜间模式下阅读。

实验器材

一部智能手机
一台笔记本电脑
边长已知的地砖铺成的地面（也可以用一把卷尺）

实验原理

众所周知，声速可以通过 $v=s/t$ 来测量得到。其中 $s$ 为声波在介质中传播的距离， $t$ 为声波传播的时间。

然而宿舍空间不足，导致 $s$ 无法很大，从而要测量的 $t$ 极短。如果直接测量声音发出的时刻与接收的时刻，两个设备之间的时间同步是一个很大的问题。

因此，我大体采用了更改距离，测量时间差的方法。让电脑固定在位置 $x_0$ 、在时刻 $t_1,\cdots t_k$ 发出声音，并让手机分别在位置 $x_1,\cdots x_k$ 处接收声音。设手机的计时起点为 $t_0$ ，接收到声音的时刻为 $t_0+t_1',\cdots t_0+t_k'$ （即从手机获取到的度数为 $t_1',\cdots t_k'$ ）。则有

x_i-x_0=v (t_0+t_i'-t_i)\qquad i=1,\cdots,k

x_i = v (t_i'-t_i) + v t_0 + x_0\qquad i=1,\cdots,k

其中 $x_i$ 借助地砖读出， $t_i$ 由电脑控制， $t_i'$ 通过手机录音后，由程序判定。通过最小二乘法，可以得到 $v$ 的估计值。

实验过程

首先预制一段声音，它包含若干次「持续 0.1 秒的正弦波+持续 0.9 秒的空白」，中途有一些额外的空白方便我移动手机的位置。

import librosa
import numpy as np
import soundfile as sf

# make a 0.1 second beep
beep = librosa.tone(3000, sr=44100, duration=0.1)
# make a 0.9 second blank
blank = np.zeros(int(44100*0.9))
beep1 = np.concatenate((beep, blank))

# repeat it 5 times and add a 2 second blank
beep5 = np.concatenate((beep1, beep1, beep1, beep1, beep1, np.zeros(int(44100*2))))
# repeat it 4 times and add a 2 second blanks before and after
beep20 = np.concatenate((np.zeros(int(44100*2)), beep5, beep5, beep5, beep5, np.zeros(int(44100*2))))
# save it
sf.write('beep20.wav', beep20, 44100)

接着确保宿舍里面没人（实验会打扰到别人，别人也会打扰到实验），然后将电脑放置于瓷砖地面上的合适位置。

打开手机录音机，在电脑上开始播放音频，趁预留的空白时间，移动手机，让麦克风位置尽量对准第一条瓷砖接缝。动作要轻，尽量减少多余的噪音。

等待电脑发出五次「哔」声，然后把手机移动到下一个接缝处。这样重复几次，得到一份录音文件。

接下来就是处理录音文件了。可以先对文件做适当的裁剪以及局部的静音，然后我使用的是 Python 来处理。

import librosa
import numpy as np
import matplotlib.pyplot as plt

y, sr = librosa.load('v6_1.mp3')

然后就是最玄学的部分。由于播放的声音频率是确定的，我们希望单独看这个频率的强度。这时需要一些玄学调参，来尝试得到比较明显的变化。注意 n_fft 不能设置得太大，否则 FFT 用到的采样数量对应的时长太长，可能导致误差。至于这么调参在学术上是否规范……我也拿不准。

import librosa.display

S = np.abs(librosa.stft(y, n_fft=32, hop_length=1))
spectrogram=librosa.power_to_db(S**2)
plt.figure(figsize=(10, 4))
plt.imshow(spectrogram, aspect='auto', origin='lower', interpolation='none')
plt.colorbar()
plt.show()

y3000 = spectrogram[5]
plt.figure(figsize=(15, 4))
plt.plot(np.arange(0,len(y3000)/sr,1/sr),y3000)
plt.show()

输出图表

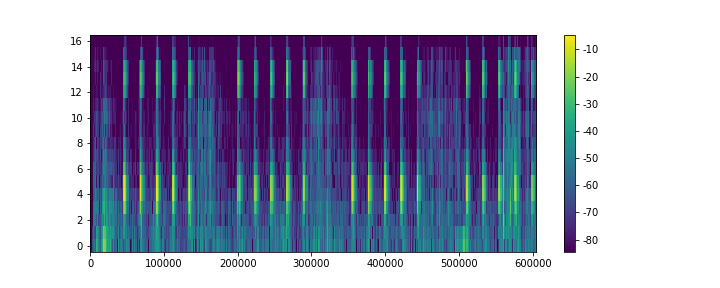
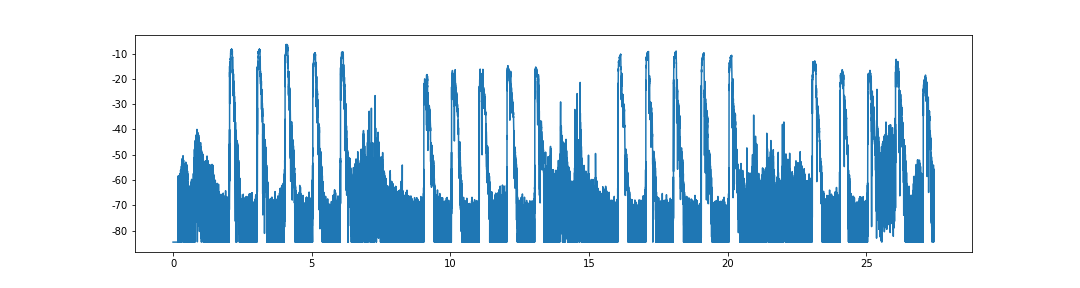
玄学的部分到这里还没有结束。我们要找到音量变化最剧烈的时刻。

top = []
rise=np.zeros(len(y3000))
for i in range(2000, len(y3000)-100):
    if y3000[i] > -30 and y3000[i] > np.average(y3000[i-300: i])+5:
        rise[i] = 1
        if not np.any(rise[i-300:i]):
            top.append(i)

top = np.array(top)
top = top/(sr/y.shape[0]*y3000.shape[0])
print(top)

输出结果为

[ 2.03877214  3.03881584  4.03876883  5.03885788  5.17364224  6.03890158
  6.17364059  6.19695121  7.28289045  9.0414363   9.14157219  9.19363559
 10.04148    10.16188796 11.04147834 11.15567317 12.04138599 12.15390281
 13.04147504 13.15362905 13.97185899 14.56754961 14.66890999 16.04396441
 17.0439174  17.1701757  18.04400645 18.16423301 18.19910823 19.04405015
 19.16849439 19.19874377 20.0440485  20.16409365 20.19878747 23.04631111
 24.04644551 24.20544751 25.04644385 25.18871119 25.20517375 25.37496939
 26.04630615 26.1857617  27.04653125 27.18861718 27.2085718 ]

这当中出现了很多明显有误的时间点，我们再筛选一遍。

top2 = []
for i in range(0, len(top)):
    if top[i] % 1.0 > 0.03 and top[i] % 1.0 < 0.06:
        top2.append(top[i])
top2 = np.array(top2)
print(top2)

得到的结果为

[ 2.03877214  3.03881584  4.03876883  5.03885788  6.03890158  9.0414363
 10.04148    11.04147834 12.04138599 13.04147504 16.04396441 17.0439174
 18.04400645 19.04405015 20.0440485  23.04631111 24.04644551 25.04644385
 26.04630615 27.04653125]

下面就是比较常规的大雾实验内容了。首先我们列出时间与距离的关系，顺便浏览一下我们具体测量到了哪些时间点。

time=top2%1.0
dis=np.array([i//5 for i in range(20)])*0.8
# 宿舍地砖的边长约为 0.8 米

plt.figure(figsize=(10, 4))
plt.plot(time,dis,'.')
plt.savefig("dis-time.png")
plt.show()
plt.figure(figsize=(10, 4))
plt.plot([i for i in range(20)],time,'.')
plt.savefig("time.png")
plt.show()

输出图表

计算一下相关系数，发现 $R^2$ 非常地大，证明我们的数据确实很漂亮（迫真），可以用线性关系来拟合。

px=time
py=dis
# 相关系数
r = np.corrcoef(px, py)
print(r)
print(r[0,1]**2)
# 结果为 0.9991872525587547

最小二乘法

from scipy.optimize import leastsq

def func(p, x):
    k, b = p
    return k * x + b

def error(p, x, y):
    return func(p, x) - y

# 最小二乘法
p0 = [1, 20]
Para = leastsq(error, p0, args=(px, py))
k, b = Para[0]
print("k=", k, "b=", b)

拟合结果

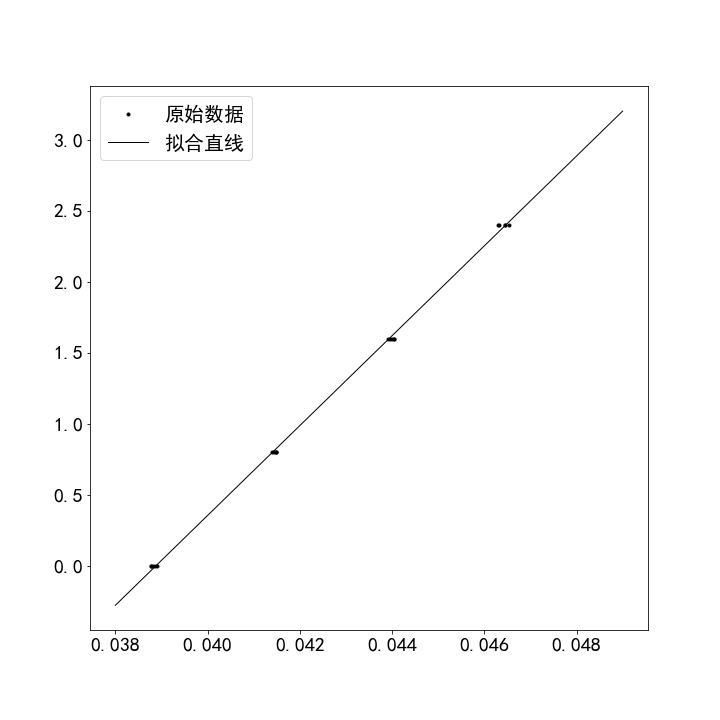
输出的 $k$ 为 $315.95855456985504$ 。也就是我们算出来声速的估计值为 $316\ \mathrm{m/s}$ 。

如果强行算 $k$ 的 B 类不确定度，结果为 $9.013115586627823\quad(P=0.95)$ 。